Agar 8 bisa disederhanakan kita jadikan bilangan 8 sebagai perkalian 4 dan 2. Untuk mengingat kembali tentang penjumlahan dan pengurangan bentuk aljabar silahkan perhatikan contoh soal berikut.
Sederhanakan Bentuk Pangkat Berikut Brainly Co Id
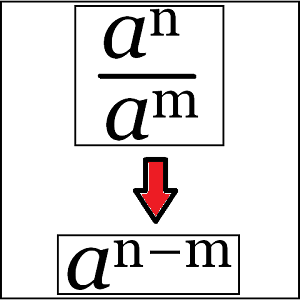
Sederhanakan bentuk penjumlahan dan pengurangan bilangan berpangkat berikut. 3p 5p 3 5p 8p 7z 3z 7 3z 4z. Bilangan berpangkat pecahan pengertian sifat rumus contoh soal dipembahasan sebelumnya kita sudah membahas materi mengenai bilangan berpangkat dan bilangan pecahan sekarang kita akan membahas materi bilangan berpangkat pecahan. Konsep penjumlahan dua bilangan berpangkat tersebut berlaku juga untuk pengurangan dua bilangan berpangkat seperti berikut. Sebelum kita mempelajari bilangan berpangkat lebih dalam maka kita harus mengetahui terlebih dahulu pengertian dari bilangan berpangkat itu sendiri baru kita mempelajari jenis dan sifat sifat dari bilangan berpangkat. Jika a p q adalah bilangan rasional dan m n adalah bilangan bulat positif dengan m n maka. Sebelumnya kita sudah mengetahui bahwa.
Sahabat matematika adalah salah satu ilmu yang diam diam memiliki manfaat atau kegunaan yang sangat penting terutama bagi para ilmuan ilmuan. Squad selain bilangan berpangkat positif dan bilangan negatif dalam matematika juga ada bilangan berpangkat nol. Berikut ini adalah pembahasan tentang bilangan bepangkat yang meliputi sifat sifat bilangan berpangkat operasi bilangan berpangkat contoh soal bilangan berpangkat contoh operasi bilangan berpangkat sifat sifat perpangkatan perkalian bilangan berpangkat pembagian bilangan berpangkat penjumlahan bilangan berpangkat pengurangan bilangan berpangkat perpangkatan bilangan berpangkat. Sebagaimana yang kita ketahui bahwasannya eksponen atau pangkat biasanya yang tercantum yaitu bilangan asli atau bilangan bulat. Operasi aljabar pada bentuk akar. Karena 4 merupakan bilangan kuadrat.
8 42 42 22 22. Sederhanakan bilangan perpangkatan perpangkatan berikut ini. Operasi aljabar seperti penjumlahan. Sebagai latihan silakan sederhanakan bentuk akar dari 12 75 125 dan 300. Dengan kedua contoh diatas sudah bisa menjelaskan tentang sifat penjumlahan dari bilangan berpangkat menggunakan bilangan pokok sama yakni. Berdasarkan sifat pembagian bilangan berpangkat positif dapat diperoleh.
Gunakan aturan di atas. Bilangan eksponen adalah bentuk pada bilangan perkalian dengan bilangan yang sama lalu diulang ulang atau singkat perkalian yang diulang ulang. Agar lebih jelasnya pelajari penjumlahan dari bilangan berpangkat berikut ini. Dan merupakan bentuk kelanjutan dari operasi hitung yang terdiri dari penjumlahan pengurangan pembagian dan perkalian. Jika a bilangan riil dan a tidak sama dengan 0 maka. Sehingga sifat untuk bilangan berpangkat nol adalah.
Bilangan berpangkat positif memiliki beberapa sifat tertentu yang dimana bilangan itu terdiri dari a b sebagai bilangan real dan m n yang merupakan bilangan bulat positif. Sifat penjumlahan dan pengurangan pada bilangan berpangkat.
Gallery of Sederhanakan Bentuk Penjumlahan Dan Pengurangan Bilangan Berpangkat Berikut
